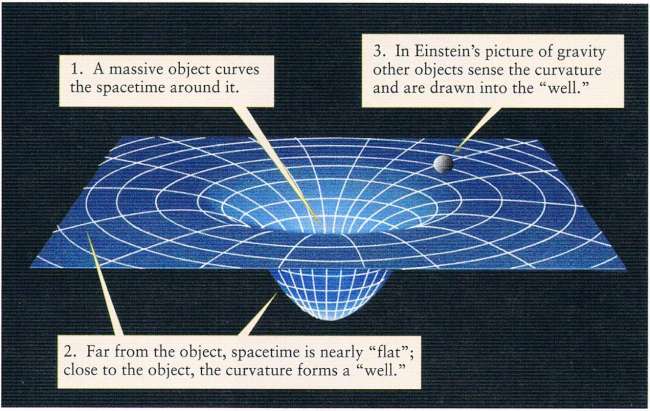
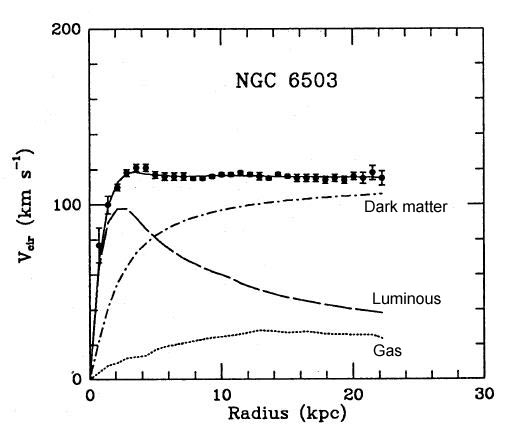
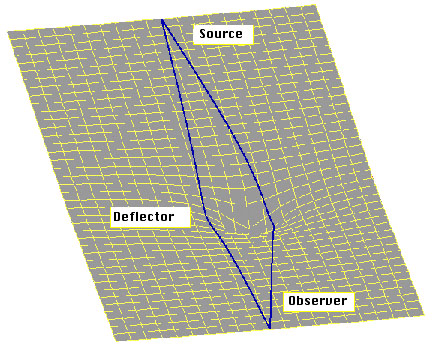
Dark MatterFor many years it was thought that all the mass of the universe was present in a form that we can detect due to its emission of electromagnet radiation. Since the 1930’s evidence has mounted that this assumption was incorrect. This change of thought was based on the observations that galaxies in clusters had orbits that could not be accounted for by the amount of luminous matter. Studies of the rotation of galaxies also indicated the presence of more matter than that observed. This lead to what is called the dark matter (DM) problem. Today we know that only 4% of matter in the universe is in a form that emits electromagnet radiation (Carrol & Ostlie 2007, 1232). Many studies have been initiated to find exactly what this matter is and how it is distributed. This article outlines how we know DM is present and how it has been detected. It also discusses candidates for the matter and what form we think it is in. Also problems with the current understanding are briefly discussed. Gravity We will soon discover that a very important part of our detection of DM is our understanding of fundamental physical principles of nature. More specifically it is the force that we call gravity that helps us locate DM in the Universe. As such it is important that we first explore our theories on the nature of gravity. If you understand Newton's and Einstein’s views on gravity you can skip this section. Following on from the empirical description of gravity by Kepler Isaac Newton discovered the fundamental principles that cause the motions described by Kepler (Freedman & Kaufmann 2008, 80 – 85). Newton found that the attraction between two objects is proportional to their combined mass and inversely proportional to the square of the distance between them. Each body feels the same force. This relationship is called Newton’s law of gravitation and is given below: F=G(m1m2/r2) F = gravitational force between two objects G = universal constant of gravity (6.67 x 10-11 m3kg-1 s-2) m1 = mass of first object m2 = mass of second object r = distance between the two objects There is a slight complication to the application of this law if we study an object orbiting within an extended massive object (for example a galaxy). If an object is orbiting within a galaxy the mass of the second object is the sum of all the matter that lies within the orbit of the orbiting object (Freedman & Kaufmann 2008, 617). The mass outside of the smaller object’s orbit has little effect on its orbit. While Newton’s law of gravity is very successful at describing the motion of objects there are some observations that it does not account for. Since the force exerted is proportion to the mass of each object the net force between two objects should be zero if one of the objects has zero mass. Photons have no mass yet they are affected by gravity as we will soon see. There are some deviations in the orbit of Mercury that Newton’s law can not fully explain (Freedman & Kaufmann 2008, 583). For an orbiting body we find that that the force of gravity is equal to force required to accelerate the body in accordance with Newton’s second law (ie F=ma). This is known as the equivalence principle (Ryden 2003, 27). It turns out than in Newton’s system the force of gravity on an object is equal to its inertia. It was this fact that led to the formation of the theory of general relativity by Einstein which will now be discussed. The effect of gravity on light and the variation in mercury’s orbit is accounted for in Einstein’s general theory of relativity. It also provides a natural explanation for the equivalence principle. The theory states that objects distort both space and time (known as space-time) around it (Ryden 2003, 29 - 30). The distortion of space-time is often illustrated by the use of a stretched sheet of rubber. When an object is placed on the sheet a depression is formed with the object at the centre (see figure 1). Figure 1: A two-dimensional representation of the curvature of space-time due to a massive object. The orbiting body follows a line of least resistance (Freedman & Kaufmann 2008, 583). In this view of gravity no forces act on objects. They simply follow a curved path that is dictated by the shape of the curvature around an object (Greene 2003, 67 – 71). For example the Earth follows a curved path around the Sun. It does not do so due to some force but merely follows the line of least resistance. The Earth also distorts space-time allowing the Moon and our satellites to orbit. As this approach does not rely on the objects having mass it is possible for light to be affected by gravity. This was a prediction of this theory that was put to the test in 1919 (Freedman & Kaufmann 2008, 582 - 583). During a total solar eclipse the effect of the Sun’s mass had on the light from stars behind it was investigated. It was found that the Sun’s mass did indeed bend light by the predicted amount. As with the Earth around the Sun light follows a curved path near massive objects (see figure 2). More precisely the light follows a straight line in space-time (BHweb). Figure 2: Illustration of light being bent due to the distortion of space-time. This results in a image of a background star being shifted ie from point A to B (CENTweb). In most situations the predictions of the motion of objects with mass are the same with either view on gravity. Newton’s form of gravity differs when objects are close to massive objects. The steep curvature of space-time renders Newton’s laws inaccurate. Newton’s view also fails to account for the affect on light. How We detect Dark Matter Now that we have a basic understanding of the nature of gravity we can start to look at how we deduce the presence of DM. Galaxy Rotation Curves The nature of gravity means that the speed that an object orbits another is dictated by the distance between the two bodies. The further the object from the central body the slower it would move. An important discovery was that objects in our galaxy do not orbit the galactic centre as we initially thought. A rotation curve (see fig 3) plots the orbit speed of objects measured outwards from the galactic centre. Data for rotation curves for our galaxy has been sourced from the study of radio emissions from hydrogen gas (Freedman & Kaufmann 2008, 617 - 619). These data shows that the rotational speed of objects do not decline towards the edge of the galaxy as expected. In fact the curve is fairly flat out to the edge of the observable galaxy. The conclusion being that there is considerable mass outside of the observable galaxy. We can only observe about 10% of the matter in our galaxy. Vera Rubin did much work on rotation curves for galaxies other than our own (Hooper 2006, 14 -16). She also studied the rotation curves for galaxy clusters. Based on her studies Rubin concluded that a large amount of invisible matter needed to be present. Begeman, Broels & Sanders (1991) present an analysis of the rotation curves of ten carefully selected galaxies. Using accurate and high resolution 21cm emission lines from neutral hydrogen they modelled the mass distribution of the galaxies. They used three parameter dark-halo models to perform this task. The three parameters used was the mass to light ratio in the visible disk, the galaxy’s core radius and the asymptotic circular velocity of the halo. For the modelling it was assumed that the halo was spherical. The study found that the predicted curve fits the measured rotation curves well. It also determined the contribution to the rotation curve of three types of matter (gas, luminous and dark matter). These curves (fig 3) show that the contribution by DM becomes dominant with increasing distance from the galactic centre. Figure 3: An example of a galaxy rotation curve studied by Begeman, Broels and Sanders (1991). The solid line is the theoretical rotation curve and the dots with error bars the measured object speed. Also shown are the contributions made to the curve by gas, luminous matter and dark matter. Galaxy motion in Clusters However, Rubin was not the first to find evidence for DM. That honour goes of Fritz Zwicky who in 1933 suggested that DM existed (Ryden 2003, 134). He based his conclusion on the study rotational speeds within the Coma cluster. He concluded that there was not enough visible matter to hold the cluster together due to their high radial velocities in the cluster. An important concept it Zwicky’s conclusion is the mass to light ratio. This is a measure of the amount of luminous material in a unit area (Ryden 2003 p 126-129). Also the gravitational mass of a galaxy cluster can be determined using the virial theorem based on their orbital velocity and radius (UNIweb). The virial theorem is based on Keplerian motion and is as below: M ∼ (2RV2)/G where M = Galaxy cluster mass R = radial distance V = orbital period G = universal constant of gravity For this to hold true the system must be in gravitational equilibrium. Zwicky found that the galaxy motions in the Coma cluster required a mass density greater that 400 times more than what was observed (KRIweb). Thus non-luminous, or DM, must be present. However, we now know that some of Zwicky’s missing mass is hot gas between the galaxies (Freedman & Kaufmann 2008, 654). This gas emits x-rays. Gravitational Lensing As light is affected by the curvature of space-time (or affected by gravity in other words) it provides a method of accurately determining the mass of massive objects. More specifically it can be used to determine the gravitational mass of an object. This is the basis of gravitational lensing. Gravitational lensing can be viewed in the same way that shaped glass refracts light. As light passes a massive object it bends in response the curvature of space-time (BERKweb). This concept is illustrated in Figure 4 below.
Figure 4: The paths of light (shown in blue) taken to form a gravitation lens. Also shown are the relationships between source, deflector and observer (Berkweb). How much a mass will deflect light is dependant only on the deflector mass and the distance at which it passes the object (Ryden 2003, 139 - 140). The relationship is given below: α = 4GM/c2b α = defection angle G = universal constant of gravity M = mass of lensing object c = speed of light b = distance between photo and object For example photons just grazing the surface of the Sun will be deflected by 1.7 arcsec (Ryden 2003, 140). The experiment in 1919 to test Einstein’s prediction found the amount of deflection was as predicted. Thus the mass of a cluster (or any other object) can be determined by the amount that it bends light from background objects. If the object is an extended object such as a galaxy cluster the path of a particular photon may be complex. As we will see shortly computer modelling is required to study images created by a gravitational lens. These simulations give us insight into the amount and distribution of DM. The Hubble Space Telescope has been used to capture images of galaxy clusters acting as gravitational lenses. One of these images is of SDSS J1004+4112 that produces five images of one quasar and distorted images of galaxies that lay behind the cluster (fig 5, NASAweb). The galaxy cluster is located seven billion light-years away from us.
Figure 5: The gravitational lensing caused by SDSS J1004+4112. There are 5 images of one quasar (one is located in the core of a galaxy) and distorted images of background galaxies (NASAweb). Detailed study of SDSS J1004+4112 have determined the distribution of matter in
the cluster. A study by Williams and Saha (2004) found that the galaxy cluster was dominated by DM. The
mass of the inner-most 100 kpc is about 5 x 1013 M Studies such as the one above are conducted using simulations of computers. There are various factors that are taken into account but the end result must match observations. With time these models have been refined and late models are able to accurately reproduce the lensed images (Oguri 2010). Oguri was able to model the SDSS J1004+4112 system such that the images of the lensed quasar and galaxies where reproduced. To achieve this factors such as the properties of the galaxy cluster and data from time delays of variations in the lensed quasar’s brightness was used to refine the model. This study found that DM was centred on the brightest galaxy in the cluster. In this manner DM can be detected and its distribution within and around galaxies and in intra-galactic space within clusters can be determined. While the gravitational lensing described above is useful in determining galaxy cluster masses less powerful lensing can also be used (Bartelmann and Schneider 2001). Unlike the multiple images and arcs formed by strong gravitational lensing objects may be distorted so subtlely that they the lensing effects are not easily recognised. This weak gravitational lensing method relies on statistical methods to measure distortions. Weak gravitational lensing therefore can be used to detect DM in clusters where strong lensing is not present. As weak gravitational lensing is a statistical method the determination of the galaxy cluster centre is important but it may be difficult to identify the central galaxy. This is where x-ray images are useful (UNIVweb). Galaxy clusters contain hot gas in the intra-galactic space that emits x-rays. The heating of this gas has occurred due to collisions. By measuring the emissions we can determine the centre of mass. With the centre of mass determined the effects of weak gravitational lensing are more accurate and the distribution of DM can be determined. An interesting application of the x-ray method of mass determination is that it can be used to determine the mass to light ratio (UNIVweb). The x-ray emission is dependant on normal matter mass. Once the gravitational mass is determined by the amount of gravitational lensing the mass to light ratio can be determined giving a measurement of the amount of DM in the cluster. Dwarf Galaxy Interactions Galaxies such as the Milky Way are orbited by dwarf galaxies (Freedman & Kaufmann 2008, 617). As they orbit tidal forces are exerted on them. This leads to the dwarf galaxy disintegrating over time leaving a steam in their path. If we can measure these tidal streams we can model the distribution of mass in our galaxy. Two examples of dwarf galaxies undergoing this process are the Canis Major Dwarf Galaxy and the Sagittarius Dwarf Galaxy which both orbit the Milky Way. The interaction between large galaxies and orbiting dwarf galaxies can indicate the presence of DM and its distribution. A study of the tidal stream left as a result of the slow destruction of the Sagittarius Dwarf Galaxy indicates that not only is DM present in our galaxy but its distribution is not quite as expected (Law et al. 2009). The study measured the three-dimensional shape of the Milky Way halo and found that it was shaped like a ‘flattened beach ball.’ Surprisingly the flattening was perpendicular to the galaxy’s spiral disk and was greater than predicted. A similar study of the Andromeda Galaxy studied red giant branch stars in a tidal stream from a previous interaction (Chapman 2005). This study found that the Andromeda DM halo was similar to that of the Milky Way. Neither the Milky Way nor Andromeda are unusual galaxies. Most if not all galaxies have similar DM halos (Ryden 2003, 133). Dark Matter Candidates There are two classes of candidates for DM. These are MACHOs and WIMPs and these will be discussed in turn. MACHOs The most obvious and instinctive candidate for DM is normal matter. A likely source of massive objects that are difficult to detect is the processes that produce stars. At the end of the life of stars a variety of objects may result as a function of their mass (Hooper 2007, 20-27). At the end of the life of a low mass star (0.4 to 4M A high mass star will end its life in a far more violent manner. These stars produce supernovae (Freedman & Kaufmann 2007, 536 - 539). The nature of the remnant is dependant on the remaining mass. It may be a neutron star or if the mass is sufficiently high a black hole. Both objects can be difficult to detect if in isolation. A condensing cloud of gas may not form a star if there is not enough material. A
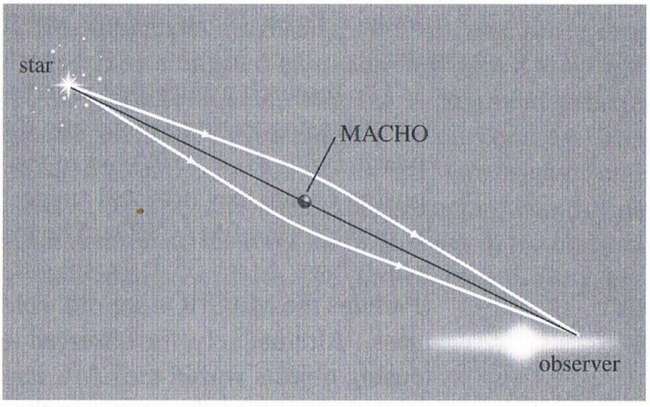
brown dwarf is formed if the body’s mass is less than approximately 0.08M These objects are examples of massive compact halo objects (MACHOs). They are objects containing normal matter. Their low luminosity makes them difficult to detect. However, their gravity can be used to detect them as they will bend light causing gravitational lensing (figure 6). It was this feature that researchers used to search for MACHOs (Hooper 2007, 36-39). The researchers looked for the brightening of background objects. More specifically they watched millions of stars in the Large Magellanic Cloud (Ryden 2003, 140). Once identified more powerful telescopes (eg Hubble Space Telescope) were be used to determine the nature of the object. A program was undertaken at the Mount Stromlo Observatory in Australia to find MACHOs and test if they contributed a significant part of DM. The study used gravitational lensing and took place between 1993 and 2003 before the observatory was destroyed in a fire (Hooper 2007, 39-40). The first image of a MACHO was taken in December 2001 by the Hubble Space Telescope and the European Southern Observatory's Very Large Telescope (HUBweb). The object is a white dwarf.
Figure 6: The gravitational lensing of a star in the Large Megellanic Cloud by a MACHO (Ryden 2003, 141). While this study did find MACHOs it did not find enough to account for the amount of DM detected in our galaxy (Ryden 2003, 140). This type of matter may account for 19% of the Milky Way’s mass. There is one other problem with the MACHO theory. In 1948 Alpha, Bethe and Gamow published a paper outlining the creation of matter shortly after the Big Bang (Hooper 2007, 40 – 41). They found that the ratios of light elements such as hydrogen, helium and lithium could be accurately modelled. The results of this modelling matched the masses of the light elements that we can observe in the Universe today. This created what is called the nucleosynthesis problem for MACHOs. The inability to find MACHOs in sufficient numbers and the nucleosynthesis problem makes these objects poor candidates for DM. They are not considered the likely source of the DM observed. WIMPs If MACHOs can not account for DM perhaps quantum mechanics can. Fundamental particles such as quarks have very short life spans (Hooper 2007, 61-62). Protons and electrons have a charge so emit detectable radiation. Therefore what we know as normal matter can not account for the DM detected. By definition weakly interaction massive particles (WIMPs) only reaction with atomic nuclei rarely and are more massive than known particles (Freedman & Kaufmann 2007, 619-621). Two WIMP candidate types will now be discussed. Neutrinos Neutrinos are fundamental particles and are described by the standard particle model (Kane 2009). As they interact via the weak nuclear force they interact with matter rarely. The chances of a single neutrino interacting with matter as it passes through the Earth is one in 100 billion (NOBweb). This makes them difficult to detect. The resolution of the Solar Neutrino problem (NOBweb) provided evidence that perhaps neutrinos are the DM that we detect. It was found that neutrinos oscillate and for this to occur they must have some mass. Shortly after the Big Bang it is thought that many neutrinos where formed (Hooper 2007, 71). In fact today there should be 10’s of millions of neutrinos in every cubic metre of the Universe to form the cosmic neutrino background. It was thought that if they were massive enough they could account for DM. Initially it was thought that there were two possible types of DM: cold and hot. Later a third type between the two was proposed (warm) and this will be discussed later. If matter is moving slowly it can clump together (Hooper 2007, 75– 78). This is what is known as cold DM (CDM). Alternatively DM can be particles travelling at high speeds. Fast moving particles are called hot DM (HDM). As neutrinos are very light they travel at almost the speed of light making them HDM. As the largest portion of the matter in the Universe is DM its nature has a great effect on the formation of structures in the Universe. Computer simulations have been carried out to determine how the Universe has evolved since the Big Bang (Freedman & Kaufmann 2008, 735 - 736). These simulations show that with CDM the formation of galaxies took place from the bottom-up leading to the formation of structures early in the Universes history. In contrast HDM causes galaxies to formed from the top-down [1]. In this situation galaxies are formed too late. The CDM models recreate the structures that we see in the Universe today. Thus being HDM neutrinos are not considered good candidates for DM. With the demise of the known neutrinos as a DM candidate there was no other particle in the standard particle that could be the mysterious DM. Thus the search for DM turned to more speculative. One area of current investigations involves a theoretical type of neutrino. Sterile neutrinos are a flavour that does not interact with the weak nuclear force (Natweb). Due to the discovery that neutrinos oscillate and as such had some mass it is proposed that a particle may be intermediate between the known neutrinos and the electron. This idea is supported by data from WMAP that suggests that four types of neutrinos are present. If these particles are real they may account for the DM in the WDM model (Kusenko 2009). WDM is intermediate between CDM and HDM (Viel et al, 2005). They may be produced due the neutrino oscillations or other processes such as inflation and Highs decay. As will be discussed in a later section the WDM theory can account for conflicts between CDM predictions and observations. However, it has been found this it is difficult to find parameters that resolve these issues simultaneously. There are two experiments at Fermilab investigating the nature of neutrino oscillations (FERMweb). The MINOS Experiment fires a beam of neutrinos at a detector 735km away in an underground mine. Evidence for sterile neutrinos is still to come but recent experiments have restricted the region to the spectrum they may occupy (NATweb). The Booster Neutrino Experiment (BooNE) is investigating neutrino mass by firing a beam of neutrinos at an 800 ton mineral oil detector (BNEweb). MiniBoone is the first part of the experiment that uses one detector. If oscillations are detected the experiment will be upgraded to two detectors. Initial data from this experiment were not encouraging (NATweb). However, later data combined with other similar experiments look promising. Supersymmetry Candidates Even though there is no evidence (other than theoretical) it thought that supersymmetry may provide candidates for DM (Hooper 2007, 85– 87). It is thought that matter (fermions) and force-carrying particles (bosons) are connected and one can not exist without the other. For every fermion there is a related boson with each having the same electrical and other properties. For example the superpartner of the electron is the selectron. However, to date none of these particles have been detected (Hooper 2007, 86– 87). If they have the same properties as the fermions then they should have been created in particle accelerators. It is possible that the symmetry is not perfect allowing for the superpartners to be more massive. In this situation the symmetry is said to be broken. The symmetry between matter and anti-matter is also broken as if it was not all matter would have been destroyed early in the Universe’s history. The supersymmetry theory provides one class of particles that provide good candidates for DM (Hooper 2007, 86– 87). This class (neutralinos) contains the photino, the zino and two Higgs Bosons. The description of these is outside the scope of this article. Neutralinos are currently our best candidate for DM (PICweb). As with neutrinos these particles are WIMPs and as such only interact with matter weakly. They only interact via the weak nuclear force and are affected by gravity. It is however a theoretical particle and is thought to be neutral with a mass of one hundred times that of a proton. If this theory is correct a billion of these particles could be travelling through our bodies every second. Neutralinos are currently being looked for in the Picasso Experiment (PICweb). This experiment uses superheated droplets of C4F10 in a detector buried underground and shielded. If a DM strikes a droplet it triggers a phase change that can be observed. To date no confirmed observations have been made. The DArk MAtter experiment (DAMA) was conducted at the Gran Sasso National Laboratory in Italy (LNGSweb). It used a combination of the Earth’s orbit around the Sun and the Sun’s orbit around the galactic centre to look for DM particles. Observations were made of how the incoming particle affected the detector material to study the nature of the particle. It had three phases. CaWO4 cryogenic detectors are being used to search for DM particles. For example the CRESST Experiment is currently being undertaken at the Gran Sasso Observatory (CRESweb). The detector uses scintillating CaWO4 crystals that are cooled to milliKelvian temperatures to reduce noise. DM particles are detected via elastic scattering after a collision with nuclei in the crystals. To further filter false signs a two channel detection system is used. Cold Dark Matter Problems Even though the CDM theory is currently the best DM theory that we have there are a few problems. As has been discussed the particles thought to comprise DM have yet to be identified and found. Their presence is only theoretical. Computer simulations involving CDM predict that the central part of galaxies should have a higher concentration of DM than other areas (S´anchez-Salcedo 2003). Observations of dwarf galaxies and low surface brightness galaxies show no such concentrations of DM. This is known as the cuspy halo problem. Computer modelling of the CDM theory makes a prediction about the number of structures formed in the Universe. While it agrees with the number of large galaxies the number of observed small galaxies is lower than expected (Mateo, 1998). Low luminous galaxies are dominated by DM and may contain a significant proportion of the Universe’s mass. These dwarf galaxies are difficult to find and the number required is not observed. This is known as the missing dwarf galaxy problem. Based on modelling the Milky Way should have 500 dwarf galaxies (Moore et al 1999). However, until recently only 11 had been observed(SCNweb). The fact that dwarf galaxies are difficult to find may explain why they had not been observed. In a study conducted at the W. M. Keck Observatory it was found that the Milky Way has more dwarf galaxies than previously observed (SCNweb). It may be that the galaxies are present in the predicted numbers. These problems pose a significant problem for CDM theory. The theory predicts certain results. If there results are not present then the theory is incorrect or at least in need of some adjustments. To get around the problems with CDM the WDM model was proposed. However, it too has problems. Warm Dark Matter v Cold Dark Matter We have seen that there are two theories on the nature of DM that are considered likely. These are WDM and CDM. With computer modelling and observations it is possible to investigate which is correct. WDM theory is based around sterile neutrinos while CDM is based around supersymmetry superpartners such as neutralinos. As discussed previously WDM can resolve some of the issues with CDM but not simultaneously with the same parameters. The problem for the WDM theory is that computer simulations show while the over-all structures are the same as the CDM simulations smoothing at smaller scales occurs. The smoothing occurs at the scale of galaxies. While this initially explained the apparent lack of dwarf galaxies it now appears that these objects are present. Observational data also appears to exclude the WDM theory as being correct. A study undertaken by Metcalf (2002) looked at quasar jets that had been gravitationally bend. This produced multiple images of the jets. As the jet images take different paths through the lensing object they could be compared to reveal small structures. This comparison showed that the light was bent in such a way that it indicated the presence of dwarf galaxies dominated by DM that is consistence with the CDM theory. As the WDM theory smoothes out small scale structures this result has dire consequences for the WDM theory. Due to the problems with WDM it is thought that DM is present as described by the CDM theory. Although that does not mean that there are not components of warm and HDM involved. For example given that the neutrino has some mass the neutrinos of the cosmic neutrino background (Ryden 2003, 66-67) must make a contribution to DM. Modified Newtonian Dynamics (MOND) Is it possible that our understanding of fundamental physics is incorrect? That is the situation put forth in the MOND theory (Milgrom 1983). In this work Milgrom proposed that our understanding of gravity was not complete. As gravity had only been verified in strong fields it is possible that the strength of the force is not linearly related to distance. Perhaps as distance increases strength of gravity decreases quicker than we think. Observations of galaxy rotations seem to support MOND (Hooper 2007, 208 – 212). However, there are problems with this theory. Larger galaxy clusters appear to have more mass than we can observe. Even when MOND is taken into consideration there is still not enough luminous matter. Detailed studies of the cosmic microwave background agree with the presence of DM. Also the MOND theory is incompatible with general relativity. Later modifications of the theory based on general relativity have been more successful. However, it is complicated and requires some DM to work. MOND is still an active area of research but it is thought that it is unlikely to be successful at resolving the DM problem. Conclusion The search for DM is ongoing and there are a number of problems. The nature of DM is still to be resolved. Current thoughts are speculative and need to be tested. Until this is answered we can not be sure that DM exists. Until DM is identified we can not be sure that our understanding of fundamental physics is correct. Current understanding is that DM is located in the halo of galaxies and between galaxies within clusters. It is thought that the Milky Way’s mass is 90% DM and similar galaxies contain similar amounts of DM. In all it is thought that only 4% of the Universe’s mass is normal matter. DM is thought to be cold, massive and, to date, theoretical particles. Theories based on CDM involving neutralinos are favoured but other theories can not be ruled out.
[1]
In the top-down scenario large galaxies fragment to form smaller ones. In contrast the bottom-up process results in
galaxies forming by the merger of smaller galaxies (Freedman & Kaufmann 2008, 661 - 662). References Bartelmann, M. & Schneider, P. 2001, Phys. Rep., 340, 291 Begeman, K. G., Broeils, A. H. & Sanders, R. H. 1991, Mon. Not. R. astr. Soc., 249, 523 BERKweb: Gravitational Lensing webpage, http://astro.berkeley.edu/~jcohn/lens.html (accessed 2 Dec 2010) BHweb: The Straightest Lines in Curved Space and Time webpage, http://www.black-holes.org/relativity5.html (accessed 29 Nov 2010)BNEweb: BooNE vs MiniBooNE webpage, http://www-boone.fnal.gov/about_boone/BvsMB.html(accessed 2 Dec 2010)Carrol, B. W. and Ostlie, D. A. 2007, An Introduction to modern Astrophysics 2nd ed., San Francisco: Pearson Education Inc.CENTweb Centauri Dreams: Is There a Flaw in General Relativity? Webpage, http://www.centauri-dreams.org/?p=10067 (accessed 3 Dec 2010)Chapman, S.C. 2005, New Astron. Revs, 49, 209 CRESweb: CRESST - Detector Concepts webpage, http://www.cresst.de/cresst.php (accessed 3 Dec 2010) FERMweb The MINOS Experiment and NuMI Beamline webpage, http://www-numi.fnal.gov/ (accessed 2 Dec 2010)Freedman, R. A. & Kaufmann, W. J. III. 2007, Universe, 8th ed., New York: W.H. Freeman & Co. Greene, B. 2003, The Elegant Universe, New York: Vintage Books Hooper, D. 2007, Dark Cosmos, New York: Harper Collins HUBweb: First image and spectrum of a Dark Matter object, http://www.spacetelescope.org/news/heic0116/ (accessed 2 Dec 2010)Kane, G. 1996, The Particle Garden, Helix Books KRIweb: Krioma.net: Dark Matter webpage, http://www.krioma.net/articles/Dark%20Matter/Dark%20Matter.htm (accessed 3 Dec 2010)Kusenko, A., 2009, New J. Phys., 11, 105007Law, D. R., Steven R. Majewski, S. R. & Johnston, K. V. 2009, preprint (arXiv:0908.3187v1) LNGSweb DAM-A Experiment webpage, http://www.lngs.infn.it/lngs_infn/index.htm?mainRecord=http://www.lngs.infn.it/lngs_infn/contents/lngs_en/public/about/ (accessed 1 Dec 2010)Mateo, M. 1998, preprint (arXiv:astro-ph/9810070v1)Metcalf, R. B. 2002, ApJ, 580:696–704Milgrom, M. 1983, ApJ, 270, 365Moore, B., Ghigna, S., Governato, F., Lake, G., Quinn, T., Stadel, J. & Tozzi, P. 1999, preprint (arXiv:astro-ph/9907411v1) NASAweb: NASA Image of the Day Gallery webpage, http://www.nasa.gov/multimedia/imagegallery/image_feature_575.html (accessed 30 Nov 2010) Natweb: Hunt for the sterile neutrino heats up, http://www.nature.com/news/2010/100317/full/464334a.html?s=news_rss (accessed 1 Dec 2010)NOBweb: Solving the Mystery of the Missing Neutrinos webpage, http://nobelprize.org/nobel_prizes/physics/articles/bahcall/ (accessed 30 Nov 2010) Oguri, M. 2010, preprint (arXiv:1005.3103v1) PICweb The Picasso Experiment webpage http://www.picassoexperiment.ca/index.php (accessed 1 Dec 2010) Ryden, B. 2003, Introduction to Cosmology, New York: Addison Wesley S´anchez-Salcedo, F. J. 2003, preprint (arXiv:astro-ph/0305496v1)SCNweb: 'Missing Dwarf Galaxy' Problem May Be Solved webpage, http://www.sciencedaily.com/releases/2007/09/070914173533.htm (accessed 30 Nov 2010)UNIVweb: Dark Matter in Distant Galaxy Groups Mapped for the First Time webpage http://www.universetoday.com/57006/dark-matter-in-distant-galaxy-groups-mapped-for-the-first-time/ (accessed 2 Dec 2010) UNIweb: Virial Theorem webpage, http://universe-review.ca/R04-03-VirialTheorem.htm (accessed 1 Dec 2010)Viel, M., Julien Lesgourgues, J., Haehnelt, M. G., Matarrese, S. & Riotto, A, 2005. Phys. Rev. D, 71, 063534Williams, L. L. R. & Saha, P. 2004, ApJ, 128, 2631 |
|
 |
All images and content are copyright. You are free to use material for private use. This does not include placing any material on other websites.